malvasia bianca

When I play a puzzle game (or do puzzles on paper), my goal isn’t to find solutions to the puzzles: my goal is to prove that there is a unique solution to the puzzle, with the production of that unique solution a side effect of that proof. This approach is so deeply ingrained into my approach to puzzles that I’d never really considered whether or not other people treat them the same way; thinking about it a bit more, I’m now assuming that I’m a bit of a freak in this regard, but I’m curious how y’all approach puzzles. (It wouldn’t surprise me if y’all were freaks, too, admittedly.)

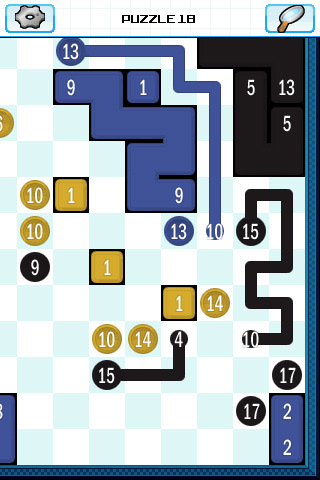
The reason why I’m bringing this up is that Piczle Lines forced me to think about what I meant by uniqueness. The game has you connecting numbers with paths of the same length: for example, if you have two 9’s, then you connect them with a path of length 9. Also, each number has a color, and you can only connect numbers with the same color. Given that, the strongest form of uniqueness would be that there is a unique set of legal paths connecting the numbers.

That turns out to be too strong, though. Say that you’ve got a 3×3 square with 9s in the upper left and lower right. Then you can fill that square with paths going up and down or paths going right and left; and, it turns out, choices like that show up all the time in Piczle Lines puzzles. While it’s possible to come up with puzzles that have a unique solution under this definition I also suspect that such a constraint would be excessively limiting.

I was going to say that the puzzles working under such a constraint would be too easy, but, actually, Numberlink does have that constraint, and my memory is that Numberlink puzzles are plenty difficult. (Incidentally, don’t be misled by the use of numbers in that puzzle, they have a completely different meaning than the numbers in Piczle Lines, but both puzzle types share other core concepts.) Still, it’s a constraint that I don’t think is inherently beneficial; I certainly enjoyed Piczle Lines more than Numberlink, though I’m now planning to revisit the Numberlink book I have.

But it’s not the only possible definition of a unique solution. The next level of uniqueness would be that there’s a unique way of pairing up the numbers, and that the regions traced out by the paths is unique. (So, returning to the example above, that those numbers would always be linked through a path tracing out the same 3×3 square.) This also turns out not to be the solution that Piczle Lines chose: fairly frequently, you’d find a decent-sized region with two pairs of numbers that could divide up a given chunk of space in multiple ways. Again, you could probably design puzzles using this form of uniqueness (though I don’t have a good feel for how that would turn out), but it’s not what we see here.

The weakest form of uniqueness uses the colors. Piczle Lines puzzles aren’t abstract puzzles, they’re drawing a picture, so maybe all solutions to the puzzle end up drawing the same color regions? For a while, I thought that this was what the game meant by uniqueness, because most of the puzzles do have a unique solution in this regard, but eventually I ran across a puzzle where you could trace out one region of the border between colors in two different ways. Still, such examples were relatively rare, and my tentative opinion is that they’re a bug: if the idea behind the puzzle is that we’re trying to make a picture, then puzzles should pin down the picture that they’re making.

My confusion about what uniqueness meant in the context of the puzzle solutions was mirrored by confusion about tactics to use. One of the quirks of the puzzles is that it was possible to leave squares blank: most puzzles filled up the entire board, but not all of them. This has an effect on how you can reason: if a corner square is filled up, for example, then there’s only one way for a line to enter and leave the corner, but what if the corner is blank?

The interesting thing about this (at least if you share my psychological peculiarities) is that you can calculate from the outset whether or not there are any blank spaces: you have enough information from the numbers alone to determine the total area traced out by the paths in the puzzle, and you can compare that area to the size of the area you have to play with. Or at least you could, if you really wanted to: it would be a pain, though. What I ended up doing was having faith that, most of the time, the puzzles would fill out the entire space, and that, the rest of the time, the blank areas would be fairly obvious, instead of isolated squares here and there. Which proved to be true, and if a puzzle did have white space, it generally came in large clumps whose borders were fairly clearly marked. (Frequently in large part by straight lines, where uniqueness is obvious.)

This same sort of calculation was also theoretically possible for smaller areas of the puzzle: perhaps there would be an area of the puzzle where you had filled out all of the boundary except for one area. Then, by calculating, you could at least figure out how much the boundary in that area extended into the surrounding region (or, conversely, how much the surrounding region pushed back into the area in question); sometimes, that knowledge alone was enough to uniquely determine where that boundary was located.

What makes this last sort of example different is that adding up the numbers inside to calculate how the boundary was shaped really could be useful. (In contrast to the whole-puzzle situation, where it’s confirming something you were almost positive was the case anyways.) I didn’t actually go to the trouble of carrying out the calculation (or at least I rarely did), but it added some real pacing to the structure of solving the puzzle: I’d get nervous if I had a large area and then would feel relieved when I got to where I understood exactly where the boundary to that region had to go.

So, in two different ways, the game managed to present me with a fair amount of uncertainty (what uniqueness meant, what the results of adding up the numbers in a region of the puzzle would be) in a way that still had some scaffolding for my desire for proof to cling to (my hypotheses of uniqueness, how I would use the result of adding if I were to carry out the exercise). And at least partly because of this, the game did quite a bit towards allowing me to push towards solutions that I couldn’t prove were unique. I’d trace out lines that seemed to make sense (but not connecting them all the way, to give me a reminder that I hadn’t proved their validity); and, once I got to a choke point for a region and could prove that the boundary had to look a certain way, being able to connect a half-dozen of uncertain lines at once felt great!

Mind you, I still spent a lot of time just staring at puzzles, not tracing out anything, looking for something that I could prove was true. Liesl noticed me playing it constantly, started playing it herself, and got just as hooked as I was, and the contrast between our styles is quite striking. She traces out lines that make sense, runs into situations where something has gone wrong, and fiddles with them until everything fits properly. So the result is that she spends a lot more time actually putting stuff on the screen than I do, spends a lot more time backtracking, and ends up getting to a solution at about the same speed as I do. (She is a rather experienced puzzle solver; incidentally, Miranda has also been known to pick up the game, it’s a good thing that we have multiple devices in the house that are capable of playing it!)

The business model for the game is a free initial download with subsequent downloadable puzzle packs available for purchase; and, in fact, one of the download packs is free. (They’ve since released another free one.) And the download packs are very cheap: you can get quick a lot of puzzles for a buck.

Also, not all puzzles are created equal: in particular, some of them fit into a story mode. Which I found surprisingly effective, despite its extremely threadbare nature (or, perhaps, not so surprising, given my “video games plots as musicals” ideas). In particular, once, I’d gone through the first chapter of story mode, and found that could buy the entire rest of the story mode (containing another hundred puzzles!) for the princely sum of ninety-nine cents, there was no question that I was going to buy it. (I’m not at all surprised that story mode was, by far, the most downloaded content pack. And yay for developers who share blog about their experiences, see here and here as well.)

And, once I’d finished those, I’d gotten more than enough pleasure out of the game to immediately buy the rest of the DLC. Who knows what the right set of price points is for this sort of content (and, if the developers are reading, I’d be happy to buy more DLC, especially if it consisted of large puzzles!), but it makes me happy that a free product that narrative hooks, free DLC to get you started, and a crystal-clear value proposition (the hardest puzzles would easily take me a half-hour or more to solve while costing just over one cent each) can lead to a good conversion rate. I just hope that the total sales are enough to keep them going!